| HIFI4ALL.DK | ||
| Avanceret model for højttalere Claus Futtrup [17.06.2013] | ||
| ||
Artiklen er primært rettet mod selvbyggere (og evt. teknikere/ingeniører), der interesserer sig for at forstå lidt mere omkring hvad der sker i højttalere. Indholdsfortegnelse:
Hvis vi ser lidt tilbage på historien kan man grundlæggende sige at Richard Small med godt held fik beskrevet en model for højttalere, som efterfølgende blev en stor succes og har været uanfægtet lige siden. Computeren er kommet til og tingene har udviklet sig lidt, men kernen er uændret. Dette grundlag bruges fortsat til beregning af højttaler-kabinetter og system udvikling. For de avancerede findes der moderne software, som kan simulere systemer mere præcist. Det hedder LEAP Enclosure Shop. Dette software blev langsomt skabt fra midt i 80'erne og fremefter og sandsynligvis har det krævet et stort arbejde at etablere de modeller, som findes i denne software, i dag i version 5. Programmet koster en pæn sum penge, men alt taget i betragtning virker det rimeligt. I løbet af 90'erne skiftede interessen blandt ingeniører fra kabinet-beregninger vha. små-signal modeller til såkaldte stor-signal modeller, faktisk ført an af en dansker, Morten Knudsen. Disse modeller søger at forklare hvad der sker når man skruer op og ned for signal styrken (og dermed lydtrykket ud af højttaleren). Jeg har p.t. endnu ikke set et stykke software der er frit tilgængeligt, som kan beregne højttaler-kabinetter med disse stor-signal modeller, men forhåbentlig kommer det. Der findes dog efterhånden en lille håndfuld programmer som på den ene eller anden måde søger at beskrive hvad der sker, når man skruer op/ned for signalet, men de koster penge og henvender sig først og fremmest til professionelle. Grundlæggende betyder dette at langt størstedelen af beregninger til højttalersystemer fortsat baserer sig på Thiele/Small modellen. Dette gælder både private selvbyggere og halv-professionelle. Desuden er det denne model, der bruges i undervisningen af nye ingeniører på universiteterne. Ikke bare i Danmark, men i hele verden. Desværre forholder det sig sådan, at Thiele/Small modellen ikke er god til at beskrive hvad der faktisk foregår når enheden monteres i et kabinet. Dette var Richard Small egentlig godt klar over, men tilsyneladende er der mange andre som har ignoreret dette. Dette skrift søger at gøre opmærksom på de misforhold som er gældende ved Thiele/Small modellen samt bringe et forslag til hvad man evt. kan gøre.
Lad os kigge lidt tilbage i historien. Richard Small præsenterer i 1973 en videnskabelig artikel i "Journal of the Audio Engineering Society" (JAES) med titlen "Vented-Box Loudspeaker Systems, Part I: Small-Signal Analysis" hvor Small i første omgang giver et kort historisk tilbageblik og derefter beskriver tabs-faktorer m.v. For mig at se er den mest interessante side i hele denne paper på side 5. Der indgår ingen matematiske ligninger eller noget i den stil. Det er her at Richard Small redegør for sine forudsætninger og for observationer – inklusive de observationer, som han indrømmer tilsyneladende er fejlbehæftede og misvisende. Link: www.aes.org/e-lib/browse.cfm?elib=1967 Richard Small skriver (kort fortalt): 1) Porttabet (givet at man anvender en basrefleksport) er typisk i området Qp = 50-100 (hvis porten er fornuftigt stor og signal-styrken holdes fornuftigt indenfor højttalerens grænser). 2) Absorptionstabet i højttaleren kan ignoreres, Qa > 100. I visse tilfælde kan Qa bringes ned omkring 30-80. Ved anvendelse af meget tykt lag dæmpning kan Qa bringes yderligere ned. 3) Lækagetabet er typisk mest signifikant med Ql = 5-20. Small skriver herefter (jeg oversætter til dansk): "Det sidste resultat er overraskende fordi de testede kabinetter var håndværksmæssigt godt byggede og synes ganske lækage-fri." Derefter skriver Small at han har tillid til målemetoden, baseret på metodens evne til at afsløre med rimelig nøjagtighed små bevidst tilførte kabinet tab, og det fører til den konklusion at den målte lækage i tilsyneladende lækage-fri systemer ikke er en målefejl men en indikation af at de faktiske tab i kabinettet ikke er konstante med frekvensen. Det er en meget interessant observation og nogle interessante tanker, som Richard Small har skrevet om her. Det vil vi kigge lidt nærmere på.
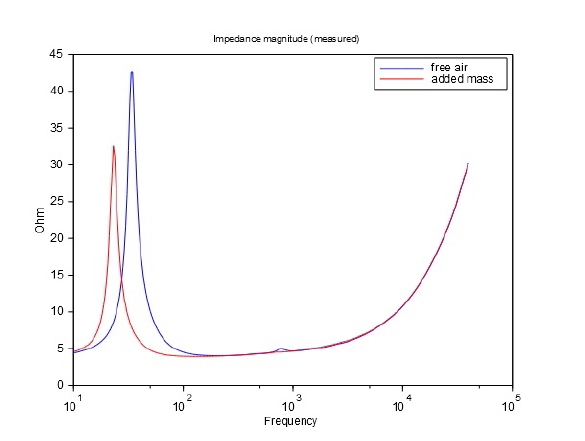
Det tab som Richard Small kalder for "ikke konstant med frekvensen" vil vi fremover kalde for frekvens-afhængig tab/dæmpning. Small har måske nok fat i noget her, men han har overset at denne frekvensafhængige dæmpning findes i enheden og ikke i kabinettet. For at overbevise læseren præsenterer jeg nu helt almindelige impedansmålinger på en højttaler-enhed. Enheden er spændt op og befinder sig i fri luft, dvs. der er p.t. ikke noget kabinet omkring enheden. Enheden måles med og uden tillægs-masse (added mass, den helt almindelige metode til bestemmelse af Thiele/Small parametre). Målingerne ser ud som følger:
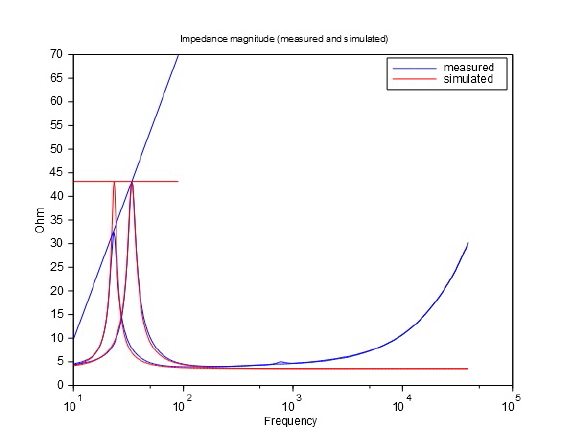
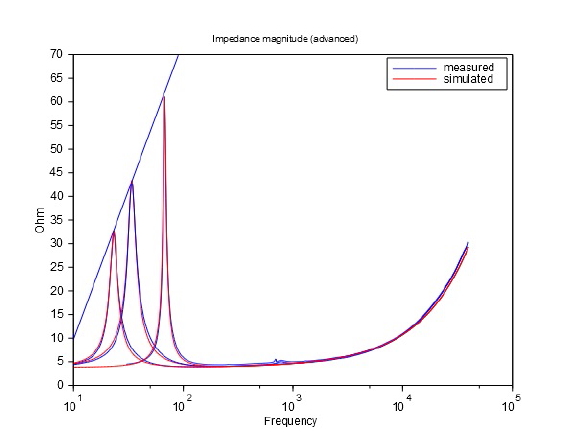
Der er som nævnt to målinger på grafen. Den ene er for enheden i fri luft (blå kurve) og den anden er tilsvarende men med ekstra masse monteret på enheden (rød kurve). Når massen monteres på enheden kan vi se at enhedens resonans-frekvens falder (top-punktet på kurven optræder ved en lavere frekvens). Det er helt almindeligt og dette benyttes til bestemmelse af enhedens fysiske parametre (bevægelig masse, Mms, samt efterfølgende til bestemmelse af motor-systemets kraft faktor, Bl). Det som man imidlertid også kan observere er at impedans-toppunktet er blevet mindre. For den blå kurve har vi at impedansen peaker ved ca. 43 ohm, men for den røde kurve peaker impedansen ved ca. 33 ohm, altså en lavere værdi. Dette indikerer klart at dæmpningen er øget. Thiele/Small modellen tager ikke højde for denne effekt. I en simulering med Thiele/Small modellen vil peak-højden være den samme med/uden added mass, hvilket tydeligt er forkert. For at overbevise læseren præsenterer jeg nu en simulering med Thiele/Small modellen sammen med de tidligere præsenterede målinger:
Som sagt tager Thiele/Small modellen ikke højde for den frekvens-afhængige dæmpning, hvilket resulterer i at peak-højden på kurven er uændret, når man simulerer at der er monteret en ekstra-masse i forhold til enheden uden ekstra masse. Lige så tydeligt er det at sådan forholder det sig ikke i virkeligheden. Man skal mildest talt være noget "skæv-øjet" for at kunne overbevise sig selv om at de blå og de røde kurver er sammenfaldende. Det er de ikke, langt fra. Dette indikerer at Thiele/Small modellen ikke passer med virkeligheden. At det forholder sig sådan generelt vil du kunne forvisse dig om ved at måle dine egne højttaler-enheder. Jeg vil påstå at alle enheder i verden udviser denne karakteristik, dvs. alle som er almindelige elektro-dynamiske enheder og som har en mekanisk masse/fjeder karakteristik. Denne lidt spidsfindige formulering af et forbehold skyldes at jeg har set højttaler-enheder som ikke udviser nogen impedans-pukkel ved resonansfrekvensen og for disse enheder vil man derfor ikke kunne observere fænomenet. Forbeholdet forekommer dog meget sjældent i praksis. Derfor er det måske ekstra overraskende at Thiele/Small modellen faktisk ikke kan simulere dette. Hvorfor har man valgt en model af højttaler-enheden, som ikke kan simulere enhedens opførsel? Jeg vil vove den påstand at det er en svipser. Der er muligvis tale om en simplificering, som ikke havde stor betydning for 50 år siden, men som i dag har fået en stigende betydning. Det vi ser på måle-kurverne, hvor impedans-puklen ved resonansfrekvensen har varierende højde, afhængigt af frekvensen, kalder vi for frekvensafhængig dæmpning i højttaler-enheden.
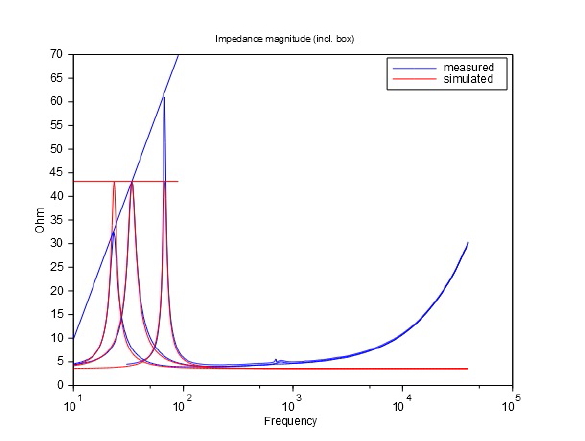
Det næste gode spørgsmål kunne være, hvad sker der i kabinettet? Hvis nu denne opførsel med frekvensafhængig dæmpning kun sker i fri luft og ikke i et kabinet, så kan Thiele/Small modellen jo godt bruges alligevel. Målinger viser tydeligt at fænomenet også findes når resonansfrekvensen øges ved at montere enheden i et kabinet (hvor kabinettet bidrager til den samlede stivhed i systemet). For at dokumentere dette har jeg fået bygget et næsten tabs-frit kabinet i aluminium, der er (TIG) svejset sammen. Du kan se et billede af selve kabinettet her:
Lækage-tab og absorptions-tab må antages at være næsten nul, dvs. vi kan antage at Ql > 100 og Qa > 100. Qp ser vi bort fra fordi det er et lukket kabinet og det har derfor ingen port. Målinger af systemets impedans kan du se på nedenstående graf (inklusive de tidligere målinger og simuleringer):
Som sagt, fænomenet frekvensafhængig dæmpning findes fortsat når enheden er monteret i et kabinet. Faktisk kan man tegne en ret linje igennem de tre målinger, hvilket indikerer at situationen er uændret af kabinettet. Vi må konkludere at Thiele/Small modellen ikke evner at simulere denne situation (et tabsfrit system). Richard Small har tilsyneladende været i en tilsvarende situation, fordi de konklusioner han drager (som tidligere er nævnt) kan kun være et resultat af tilsvarende observationer. Hvordan skulle man ellers komme til den konklusion at tab i systemet ikke er konstant med frekvensen? Hvor kommer disse tanker fra? Jo, de må være resultatet af målinger på en højttalerboks hvor impedans-peaket er større end der simuleres med et tabs-frit system i henhold til Thiele/Small modellen. Når man simulerer et tabsfrit system, men alligevel får endnu mindre tab end intet tab, så kan man fantasere om negative tab, eller om evigheds-maskiner, eller man kan søge efter en mere nærliggende forklaring, som f.eks. at tabet varierer med frekvensen. Den eneste "fod-fejl" som Richard Small har begået, er at søge forklaringen i nogle fænomener der opstår i kabinettet, men som vi allerede har observeret i figur 1, så optræder fænomenet også i fri luft (med/uden added masse) og med vores eksperiment med et tabsfrit kabinet og dæmpningen i kabinet kan vi konkludere at kabinettet ikke spiller nogen rolle i denne sammenhæng. Hvis vi skal gøre noget for at rette op på dette, skal vi således kigge på modellen for højttaler-enheden.
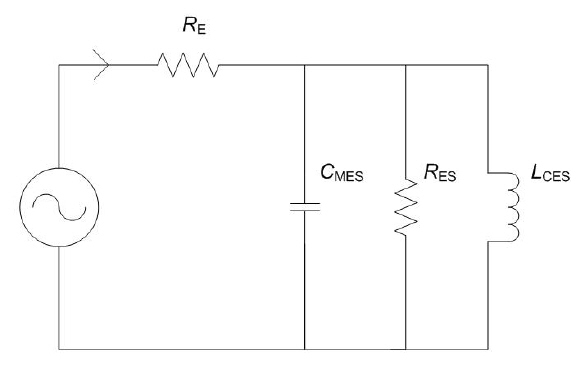
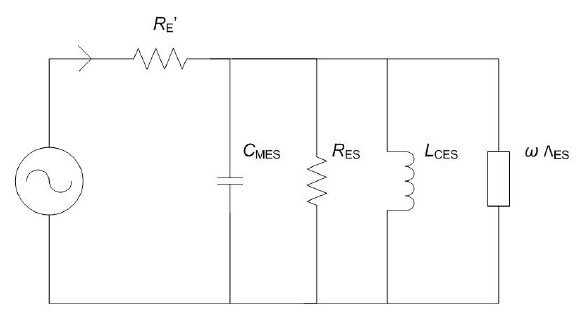
Den model for højttaler-enheden, som bruges i Thiele/Small modellen, kan beskrives med et elektrisk ækvivalent-diagram, som ser sådan her ud:
Modellen beskrives ofte løseligt som Thiele/Small modellen, men for at være retfærdig bør vi huske at dette diagram allerede blev præsenteret længe før. Den præcise introduktion i højttaler-sammenhæng kender jeg ikke, men f.eks. ses ækvivalent-kredsløb i Harry F. Olsons bog "Elements of Acoustical Engineering" fra 1947. Efterfølgende i Leo L. Beraneks bog "Acoustics" fra 1954, hvor disse kredsløb spiller en fremtrædende rolle. Vi kan altså ikke beskylde hverken Neville Thiele eller Richard Small for at have etableret en forkert model for højttaler-enheder. Den var etableret i forvejen. Thiele og Small har blot fortsat med at bruge denne velkendte model. Kæden er hoppet af undervejs og man har ikke iagttaget begrænsningerne i den anvendte model. Hvis vi skal prøve at rette op på denne fejl, skal vi starte med at observere at den eneste komponent i ovenstående kredsløb, som skal ændres på er dæmpnings-modstanden Res. Hvis man regulerer på Res afhængigt af frekvensen, kan man få meget god overensstemmelse med målingerne. Nu kunne man for så vidt vælge at droppe ækvivalent-diagrammet helt og f.eks. skifte til en helt anden type model. Det kunne f.eks. være nærliggende med en tidsdomæne-model, dvs. en tilstands-variabel model (engelsk: state-variable model), der inkluderer avancerede fænomener som visko-elasticitet. Lad os lige slå lidt koldt vand i blodet og prøve at rette op på det her på en helt enkel måde, så tingene ikke bliver unødigt komplicerede. Løsningen er at indføre en modstand parallel med Res som er frekvensafhængig. Vi definerer således Raes = Aes * omega, hvor omega er vores frekvens-afhængighed og Aes er en mekanisk admittans som på en simpel måde relaterer sig til visko-elasticitet. Kredsløbet kommer nu til at se sådan her ud:
Den samlede dæmpning i systemet består nu af en kombination af de to modstande, Res og Raes, hvoraf den første er en konstant dæmpning og den sidste er lineær frekvensafhængig. Jeg vil vove den påstand at med ovenstående kredsløb kan alle højttaler-enheder nu simuleres rimelig korrekt, således at de simulerede impedans-kurver kommer til at ligge oven i måle-data og man vil stort set ikke kunne skelne de to kurver fra hinanden. I hvert fald så længe vi bliver ved de samme forudsætninger om små signaler. For at dokumentere dette for læserne har jeg simuleret enheden som er brugt til de tidligere viste målinger med ovennævnte model, der inkluderer frekvensafhængig dæmpning. Det ser sådan her ud:
Der ses nu en meget bedre overensstemmelse mellem simulering og måling. Det er lidt mærkeligt at man ikke har set denne slags modellering forsøgt for længe siden. I branchen har man vel været klar over det her i mindst 30 år. En af forklaringerne skal muligvis findes i det faktum at Raes er en meget mærkelig komponent, fordi den er resistiv og alligevel stiger med frekvensen. En sådan komponent findes ikke i elektrikernes værktøjskasse. En lille side-bemærkning. På simuleringen er der inkluderet en model for induktionen i højttaleren og derfor passer kurverne sammen også ved højere frekvenser. Det vil komme for vidt at gå ind i detaljerne omkring dette i denne her sammenhæng, men detaljerede studier viser at man er nødt til at have en god model for induktionen for at få de rigtige mekaniske data frem ved lave frekvenser. En anden side-bemærkning. På simuleringen i box er der inkluderet et absorptionstab med Qb = 109. Det viser sig at dette tab, hvor lille det måtte synes at være, er ret vigtigt for at få impedans peaket til at passe. Absorptionstabet er for et tomt kabinet (uden dæmpningsmateriale) og jeg vurderer at tabet opstår pga. selve enheden (som i sig selv er en imperfektion ift .det perfekte kabinet), dennes membran og gummikanten. Når jeg tidligere i min karriere har forsøgt at tage diskussionen op med mine kollegaer omkring det mærkelige at dæmpningen ændrer sig, når der lægges en ekstra masse på membranen, har mine kollegaer generelt svaret henkastet at årsagen skyldes noget i stor-signal domænet, dvs. afhængigt af input-signalets størrelse. Det er for så vidt korrekt at fænomenet ligger udenfor hvad der kan simuleres med den simple model, men det er forkert at det har noget som helst med stor-signal at gøre da fænomenet kan observeres ved alle signal niveauer. Det er ganske enkelt en fejl/mangel ved den simple små-signal model.
Der er mange konsekvenser af det vi netop har observeret og konkluderet. Den første observation er at Richard Small har blandet dæmpning i enheden med sine konklusioner omkring dæmpning i kabinettet (Qp, Qa og Ql), jævnfør tidligere nævnte 3 konklusioner. Richard Small er sådan set godt klar over det, men kun indirekte fordi han ikke betragter tabet i enheden men kun taler om tabsfaktorer i kabinettet. Han skriver omkring sammenblanding af tabs-faktorer (jeg oversætter): "Til slut, og ikke overraskende når figur 4 tages i betragtning, er det vist at tilnærmelsesvis lige store værdier for Qa og Qp i det område som normalt måles i praktiske kabinetter har en kombineret effekt på system responsen som ikke kan adskilles fra den samme totale værdi for Ql." Med andre ord, Richard Small konkluderer at vi skal glemme Qa og Qp, samt sætte Ql = 7, hvilket er velkendt i højttaler-sammenhæng (Beranek nævnte sågar Ql = 7 i sin bog fra 1954). Richard Small har været meget grundig i sit arbejde og denne vejledning er stadig gældende, hvis man ikke retter op på den forkerte model for højttaler-enheden. Hvis man derimod ønsker at udvide modellen for højttaler-enheden, så denne simuleres korrekt, kræver det samtidig at man dropper den gamle tommelfinger regel om at Ql = 7. I stedet skal man anvende det fysisk korrekte lækage-tab (som kan være meget lille, dvs. Ql bliver meget stor) og da det kan eftervises at sammenblandingen med enhedens dæmpning er gået ud over Richard Smalls bestemmelse af absorptions-tabet, vil det være netop dette tab, som skal frem i søgelyset. Absorptionstabet Qa kan sættes til en arbitrær værdi, f.eks. 7 eller 10, nøjagtig som man tidligere har antaget dette tab stammede fra lækage, men det vil nok rumme en fejl, da den tidligere sammenblandede Ql-værdi overhovedet ikke har iagttaget dæmpningen i selve enheden. Det rokker dog ikke ved det faktum at absorptionstabet reelt er det dominerende tab i et højttaler-kabinet. Det mest korrekte vil være at etablere en decideret dæmpningsmodel og indføre denne i kabinet-simuleringerne. Med en sådan dæmpningsmodel opnår man desuden at kunne simulere regulering af dæmpningen i kabinettet og kunne se effekten af sådanne variationer. Der er en fundamental meget vigtig observation i ovenstående konklusioner, nemlig at enten gør man ingenting, eller også gør man begge ting. Både enhedsmodel og kabinet-model skal ændres, samtidig. Hvis man ikke iagttager dette, men kun forbedrer den ene side af systemet, vil det samlede system blive DÅRLIGERE simuleret. Dette er konsekvensen af det grundige arbejde af Richard Small. At dette ikke respekteres og at ingeniører ofte fejlagtigt forsøger at forbedre kun den ene side af systemet er en fejl som man observerer ganske ofte. Som eksempel ynder jeg at nævnte Douglas Hurlburt, der fik sin model offentliggjort i det ansete videnskabelige tidsskrift, Journal of the Audio Engineering Society. Se: www.aes.org/e-lib/browse.cfm?elib=12074 Man ser tydeligt i Hurlburts videnskabelige artikel, at han inkluderer effekten af dæmpningsmateriale, men samtidig bruger han Thiele/Small modellen. Hurlburt er ikke alene, f.eks. har jeg set at Jörg Panzer har udarbejdet et meget avanceret stykke software til simulering af kabinetter, men forespurgt hvilken enheds-model han bruger, svarede han kækt at han bruger Thiele/Small modellen. Det kan for så vidt være OK, men så kan hans avancerede software ikke tillade sig at inkludere absorption i simuleringerne, men skal i stedet kompensere med lækage - og helt ærligt er jeg usikker på om han har gennemskuet dette. Det vi kan lære er, at selv meget avancerede matematiske modeller (som f.eks. Finite-Element modeller) kan være behæftet med fejl, hvis man ikke iagttager den simple sammenhæng der er redegjort for i denne tekst, nemlig at modellen for højttaler-enheden og modellen for kabinettet skal parres, så de passer sammen.
Jeg kender kun ét stykke software, som korrekt tager hånd om enhedens dæmpning og samtidig korrekt håndterer kabinettets dæmpning. Dette software har jeg allerede nævnt tidligere og det hedder LEAP Enclosure Shop v5. Modellen i dette program er dog noget mere avanceret end hvad der er præsenteret her. For at fremme forståelsen af hvad der virkelig sker i højttalere har Scan-Speak ud over udarbejdelsen af en små-signal model for ”avancerede parametre” implementeret disse parametre på alle enheder i kataloget. Hvis du således ser på et datablad fra Scan-Speak vil du på bagsiden kunne se diagrammet og parametrene. Desuden har Scan-Speak kvit og frit stillet et simpelt Microsoft Excel regneark til rådighed. Enhver kan downloade dette regneark og i Excel (helst version 2007 eller nyere) regne på højttaler-kabinetter i kombination med de avancerede parametre for enhederne. Du kan finde det her: I dette skrift har jeg forsøgt at gøre informationerne let forståelige ved ikke at præsentere et kompliceret formel-apparat. Dette kan du i stedet finde i ovennævnte Excel regneark. Formlerne er frit tilgængelige. I stedet har jeg i dette skrift argumenteret min sag vha. måledata samt tilhørende simuleringer og jeg håber at dette har gjort det meget tydeligt for enhver hvorledes Thiele/Small modellen er begrænset og reelt ikke præsenterer den fysisk korrekte sammenhæng, samt gjort det tydeligt hvorledes man skal være meget forsigtig med at sammensætte modeller (jf. Hurlburt) uden at man i det mindste efterfølgende verificerer sin model i en eller anden grad. Jeg er bekendt med ét stykke software, som er frit tilgængeligt, der har implementeret den små-signal model som er præsenteret i dette skrift. Programmet kan måle højttalerenheder og beregne de avancerede parametre mv. Jeg har dog ikke personligt kontrolleret resultaterne og kan ikke garantere at data er valide. Det hedder Room EQ Wizard (REW) og kan downloades her: www.hometheatershack.com/roomeq/ Skulle du have interesse for at gå mere i dybden med den præsenterede model + den tilhørende model for induktion (ikke behandlet i dette skrift), vil jeg anbefale at du kigger på min hjemmeside for yderligere information: www.cfuttrup.com/papers.html Skulle der være kritik, kommentarer eller spørgsmål er du velkommen til at skrive en email direkte til mig og desuden vil jeg forsøge at følge lidt med i Hifi4all forumet og derigennem svare på spørgsmål.
| ||
Udskriften er kun til privat brug - anden brug kræver skriftlige aftale med HIFI4ALL.DK! Copyright © HIFI4ALL.DK- Alle rettigheder forbeholdes. |